三種形式的浮置式軌道結構的模態對比分析

2017-02-05 by:CAE仿真在線來源:互聯網

1三種浮置式軌道結構的結構特點

1.1浮置式梯子型軌道結構

浮置式梯子型軌道是一種新型的浮置式軌道系統,其軌枕是由PC制的縱梁和鋼管制的橫向連接桿構成的,形似扶梯( ladder) ,因此稱之為梯子型軌枕。它是縱向軌枕的一種,既能夠發揮軌枕的特性,大幅度提高荷重的分散能力,又可補充鋼軌本身的剛性和質量的性能,可以說是軌枕的一種革新形式。特別是無碴整體道床浮置式梯子型軌道,不但充分發揮了復合軌道高剛性的特點,還使軌道構造具有充分的彈性,利用減振材料等間隔支撐結構,使其浮于混凝土整體道床之上,實現了輕量級質量彈簧系統的構想,達到了減少支撐彈簧數量的目的。這種設計,還可以大大地減小結構噪聲,成為一種“低噪聲、低振動的軌道構造”。在我國,梯形軌道已經用于高架橋的減振,并且取得了很好的效果。由于浮置式梯子型軌道的新興性,它的各種參數都與以往軌道結構的參數不一樣,其中,(1)浮置式梯子型軌枕的長度,最短為5m,用2.5米作為序列間隔,理論上長度是沒有限制的,施工方法是限制其長度的重要參數;(2)承擔聯結功能的構件使用厚壁鋼管(直徑0.08m,壁厚9mm),每間隔2.5米(是橫向軌枕的4倍)配置厚壁鋼管;(3)浮置式梯子型軌道的板下支撐屬于間隔式支撐,一般情況下支撐間距在1.2m~1.8m范圍內,由于浮置式梯子型軌道自身重量輕,所以板下支撐材料的靜剛度每延米一般在15KN/mm以上,浮置式梯子型軌道的具體形式如圖1所示。

圖1 浮置式梯子型軌道系統圖2 浮置板軌道系統示意圖

如果將整體道床與基礎結構分離,作成具有足夠剛度和質量的道床板,再浮置于彈性元件上,即構成浮置板式軌道結構。它是一種質量一彈簧隔振系統,是目前軌道交通中減振效果最好的措施。其基本原理就是在軌道上部建筑和基礎之間插入一個固有頻率很低的線性諧振器,防止振動透入基礎。該系統主要包括浮置板、板下彈性阻尼元件、側向墊板和縱向墊板。在我國,浮置板軌道已經大量應用于城市之中各種對振動以及噪聲要求較高的建筑區間或者構筑段,并且取得了非常優異的效果。而作為這種減振降噪原理的產生與其固有的屬性是分不開的,其自身的特點很多包括(1)浮置板軌道結構按照道床板的施工方法可分為現澆和預制兩種,而且長度幾乎沒有限制,現在工程中最短的預制板已經達到1.2m,而由于施工方法的限制,最長的預制板一般在30米左右;(2)浮置板軌道主要是依靠質量減振的,所以其寬度較大,一般在3.2m左右;(3)浮置板軌道的板下支撐也屬于間隔式支撐,一般情況下支撐間距在1.2m~1.8m范圍內,由于浮置板軌道自身重量較重,所以板下支撐材料的靜剛度每延米一般在7KN/mm~20KN/mm范圍內。浮置板軌道具體形式如圖2所示。

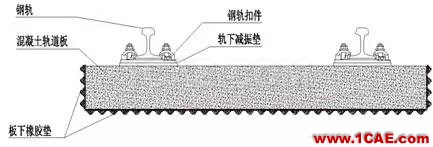
1.2道床墊軌道結構

道床墊軌道結構與浮置板軌道結構的減振原理及其類似,所不同的是它的軌道板下所采用的是整體連續式的支撐方式,用整體式的減振橡膠墊代替了單點式的鋼彈簧。目前來講,道床墊軌道結構在我國應用的還較少,效果暫時還不能確定。同時它自身也有許多特點,如(1)軌道板的外形尺寸與隧道斷面相配合,以獲得較大的質量;(2)長度宜長,以減少接頭數量,提高減振效果,若考慮維修性,可設計為短板結構;(3)采用整體支承方式,道床墊的支撐剛度一般在0.01N/mm3左右,包括側邊支承,過渡段采用不同型號的減振墊配合使用實現采取措施保證排水和防塵。道床墊軌道的具體形式如圖3所示。

2三維有限元模型的建立

2.1模態分析原理

浮置式軌道結構系統可離散為一種具有n 個自由度的線彈性系統,其運動微分方程為:

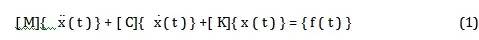
式中, [ M ] , [ C] , [ K]分別為質量、阻尼、剛度的實對稱矩陣, [ M ]為正定的,

[ C] 、[ K]為正定或半正定的; { x ( t ) }為偏離原平衡位置的廣義位置向量。當[ M] 、[ C ] 和[ K] 已知時, 即可求得一定激振力{ f }下的結構位移響應{ x} ({ x}是不隨時間變化的待定向量) 。式(1) 兩邊經傅里葉變換后,可得:

式中Φa j、Φbj為a、b 點振型元素。由上可得,n個自由度浮置式軌道結構系統的頻率響應,等于n 個單自由度系統頻率響應的線性疊加。對浮置式軌道結構進行一點激勵,多點測量響應,即可得到傳遞函數矩陣的某一列,進而計算出模態參數。

2.2模態分析的有限元模型

建立浮置式軌道系統三維有限元模型時,既要如實地反映各種浮置式軌道系統實際結構的重要力學特性,又要盡量采用較少的單元和簡單的單元形態, 以保證有較高的計算精度并減少計算工作量。其計算結果的可信度直接受合作模型、模態參數、網格劃分、約束條件等與實際的軌道結構力學特性符合程度的影響。據此,本文建立如圖所示模型。在模型中,各種浮置式軌道結構均以實體模型進行處理;每個鋼彈簧支座和橡膠支座以及扣件都作為一個彈簧阻尼單元來考慮;鋼軌以三維梁單元來模擬,相鄰扣件之間的鋼軌作為一個梁單元。在加載過程中,為了在后處理器中能查看到各種浮置式軌道結構的振型,本文進行了擴展振型,且模態擴展前指定擴展的模態數為6;各種浮置式軌道結構模態分析的荷載取零位移約束荷載。

2.3三維有限元模態分析的參數

(1)梯子形軌道板:(整體)長×寬×高=6.15 m ×2m×0.175m;(單個軌枕)長×寬×高=6.15 m ×0.56m×0.175m;彈性模量為30GPa,泊松比為0.2,密度為2500kg/m3;連接鋼管長直徑為0.08m,端部閉合梁長×寬×高為0.88m×0.2m×0.175m。

板下單個鋼彈簧靜剛度:15kN/ mm(鋼彈簧布置間距為1.2m,故板下總支撐剛度:210kN/ mm);扣件:鋼度( K) = 20 kN/ mm;軌下膠墊靜剛度:(K)=60 kN/ mm;

鋼軌: 質量( m) = 60 kg/ m; 截面面積( A) =77. 45 cm2 ;截面慣性矩( Iz ) = 3217 cm4 ; E = 210GPa ,μ= 0. 3。

(2)浮置板:長×寬×高= 7.2 m ×3.2m×0.25;彈性模量( E) = 30 GPa ;

泊松比(μ) = 0.2 ; 密度為2500kg/m3;

板下單個鋼彈簧靜剛度:7kN/ mm(鋼彈簧布置間距為1.2m,故板下總支撐剛度:98kN/ mm);扣件:鋼度( K) = 20 kN/ mm;軌下膠墊靜剛度:(K)=60 kN/ mm;

鋼軌: 質量( m) = 60 kg/ m; 截面面積( A) =77. 45 cm2 ;截面慣性矩( Iz ) = 3217 cm4 ; E = 210GPa ,μ= 0. 3。

(3)橡膠墊軌道板:長×寬×高= 7.2 m ×3.2m×0.25;彈性模量( E) = 30 GPa ;

泊松比(μ) = 0. 2 ; 密度為2500kg/m3;

板下整體橡膠墊靜剛度:0.01N/ mm3(橡膠墊為整體連續鋪設,故板下總支撐剛度:230 kN/ mm);扣件:鋼度( K) = 20 kN/ mm;軌下膠墊靜剛度:(K)=60 kN/ mm;

鋼軌: 質量( m) = 60 kg/ m; 截面面積( A) =77. 45 cm2 ;截面慣性矩( Iz ) = 3217 cm4 ; E = 210GPa ,μ= 0. 3。

為了更好地確定三種浮置式軌道結構的參數對結構振動特性的影響,(1)軌道板長度分別取7.2、15、25m;(2)軌道板厚度分別取0.25、0.35、0.45m;(3)扣件剛度分別取20、40、60 kN/ mm;通過以上三種參數對各自模態的影響定性的得到各自的模態特性,而后再進行對比分析。

3計算結果及分析

結構模態是振動系統特性的一種表征。輸出模態參數主要包括固有頻率和振型。由此可得到兩種浮置式軌道結構在激振力作用下以及在不同參數變化的影響下產生共振的固有頻率和在各階頻率下結構的相對變形(即振型)。

3.1固有頻率的對比分析

浮置式軌道結構是將具有一定質量和剛度的混凝土道床浮置在隔振器上,構成質量—彈簧—隔振系統。根據理論分析可知, 盡管浮置式軌道結構具有很多高階振動模態,但當列車通過時對隔振效果起關鍵作用的是浮置式軌道結構系統的固有振動頻率,尤其是低階固有頻率。為此,本文計算了三種浮置式軌道板在各種不同參數影響下的前6階固有頻率, 結果如表所示:三種浮置式軌道結構的前6階固有頻率,對比結果如表1到表3所示。

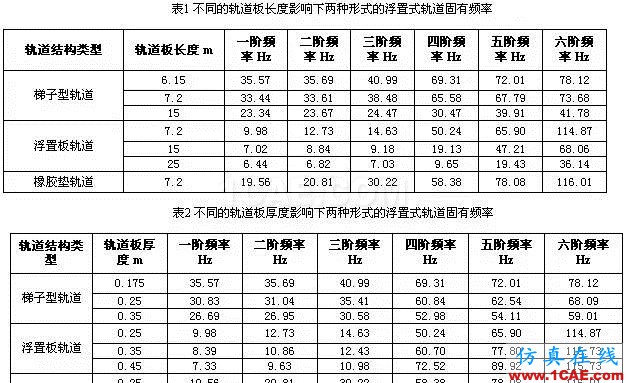
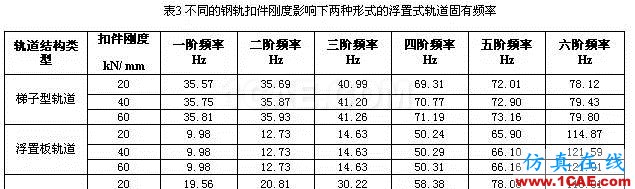
從表1~表3以及圖4~圖6中可以得出:三種不同形式的浮置式軌道結構的相似之處表現為:①三者的固有頻率都是與軌道自身結構每延米的質量有關,在其他參數不變的條件下,質量越大,固有頻率越低;②三者的固有頻率同時也和軌道板下減振結構的支撐剛度有關,在其他參數不變的情況下,支撐剛度越小,固有頻率越低;③三種形式的浮置式軌道固有頻率都隨著鋼軌扣件剛度的增加而稍有增大但變化不明顯,這說明鋼軌扣件剛度的變化對于浮置式軌道的固有頻率影響并不是很大,但是在條件允許的情況下應盡可能的選擇較小剛度的扣件,從而達到降低軌道板的固有頻率的目的。

3.2振型的對比分析

振型是每一結構所固有的振動表現形態,是結構各點相對振動量之間的關系, 它不隨測試條件和測試方法的改變而改變。通過HyperView軟件可以分別顯示兩種浮置式軌道結構的振型。由于相對于每一種軌道結構的同階振型的變形趨勢都是一樣的,所以本文只對比分析了三種浮置式軌道結構系統在所有外部參數都相同的條件下的前6階振型的瞬時圖畫(振幅),由于篇幅有限,本文只截取第五階與第六階振型圖,如圖7和圖8所示。

振型是結構的相對變形,反映了結構所固有的振動表現形態。通過有限元軟件獲得的振型,展示了浮置式軌道結構的固有振動形態,為分析浮置板軌道結構振動狀態和系統的設計及改進設計提供了理論依據。

4結語

從對三種不同形式的浮置式軌道結構的模態分析結果得到了三者前六階的固有頻率和振型,對各階振型分析得出:在滿足其他外部條件的情況下,浮置式軌道結構應優先選擇每延米質量較大、板下減振材料剛度較小、鋼軌扣件剛度較小的形式來降低各階固有頻率。而從三者振型的對比分析中我們發現:單就軌道板的變形而言,三者大體相似。而此結果同時為浮置式軌道的其他動力特性的分析如諧響應、頻譜分析等提供了一個關鍵的模態參數。

開放分享：優質有限元技術文章,助你自學成才